Как делать наклоны: Наклоны вперед — как правильно делать, видео техники выполнения — AtletIQ.com

Упражнение наклоны вперед для идеальной растяжки и гибкости

От ступней до макушки — эффективное упражнение наклоны вперед из разных позиций идеально подходит для улучшения гибкости и мобильности мышц и сухожилий. Рассказываем подробно о технике выполнения.

Теги:

Здоровье

Похудение

Фитнес

Идеальная фигура

Домашние тренировки

Shutterstock

Уделяйте внимание не только силовым тренировкам, но и расслабляющим занятиям на растяжку. Наклоны вперед — подходящий вариант для развития гибкости ног, ягодиц, рук и спины. Залог успеха — правильная техника. Пошагово выполняйте каждое упражнения – и идеальная растяжка ваша. Можно повторять упражнения после активной силовой тренировки. 

Наклон головы вперед 

Чуть смещенная осанка вперед — проблема многих. Наклоны головы корректируют неправильное положение и избавляют от неприятных болей в шее и спине после рабочего дня. 

Техника выполнения:

1. Сначала подтяните подбородок двумя пальцами одной руки.

2. Положите другую руку на затылок и мягким движение надавите на голову и опустите ее вниз, как будто вы тяните ее к груди. 

3. Когда вы почувствуете растяжение в задней части шеи, зафиксируйтесь в положении на 20-30 секунд. Повторите упражнение 5 раз. А затем сделайте наклоны без помощи рук еще 10 раз. 

Наклон вперед из положения сидя

Наклоны головы и туловища вперед помогут растянуть заднюю часть тела, раскрыть бедренные суставы и немного расслабиться. 

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Техника выполнения:

1. Сядьте на пол и вытяните ноги прямо перед собой. Чтобы было удобнее выполнять упражнение «наклоны вперед», положите под ягодицы тонкое одеяло.  

2. Сделайте вдох, согните правое колено и подтяните пятку к ягодицам, чтобы получилась поза полубабочки. Слегка прижмите правую ступню к внутренней части левого бедра, а левую руку положите рядом с бедром на пол. 

3. Выдохните и слегка повернитесь туловищем влево. Вытяните позвоночник и лягте животом на выпрямленную ногу. Если вам сложно доставать руками до пятки, возьмите специальный ремешок и захватитесь им. 

4. На выдохе старайтесь уйти дальше к пяткам, но без резких движений. Когда вы держитесь за пятку, разводите локти в сторону и сохраняйте спину прямой. 

5. Оставайтесь в позе от 1 до 3 минут. Затем на выдохе медленно вернитесь в исходное положение и поменяйте ногу. Для начала можете попробовать наклоны туловища вперед с обеими выпрямленными ногами. 

Наклон вперед из положения стоя на гимнастической скамье 

Известное многим упражнение до сих пор — один из основных пунктов ГТО. Главная ошибка при выполнении — сгибание ног в коленях. Так что лучше наклоняться до своего максимума, но с прямыми ногами. 

Техника выполнения:

1. Встаньте на гимнастическую скамью с ровной спиной и выпрямленными ногами. Не забудьте предварительно разогреть мышцы.

2. Поставьте ноги вместе и разверните руки ладонями от себя.

3. Начинайте медленно округлять спину и наклоняться вниз. Старайтесь не просто коснуться ладонями носков, но и опуститься ниже уровня скамьи. Помните, сгибать ноги нельзя. Опускайтесь на выдохе и фиксируйтесь в каждой точке на несколько секунд. Опускайтесь медленно без рывков. 

Регулярные тренировки не только ключ к идеальной фигуре, но и профилактика различных заболеваний. Занимайтесь любым приятным для вас спортом, чтобы улучить самочувствие и побороть стресс. Если вы хотите похудеть, помните — одного спорта не достаточно. Решающий фактор набора веса — рацион. Так что считайте калории и отказывайтесь от вредных продуктов. 

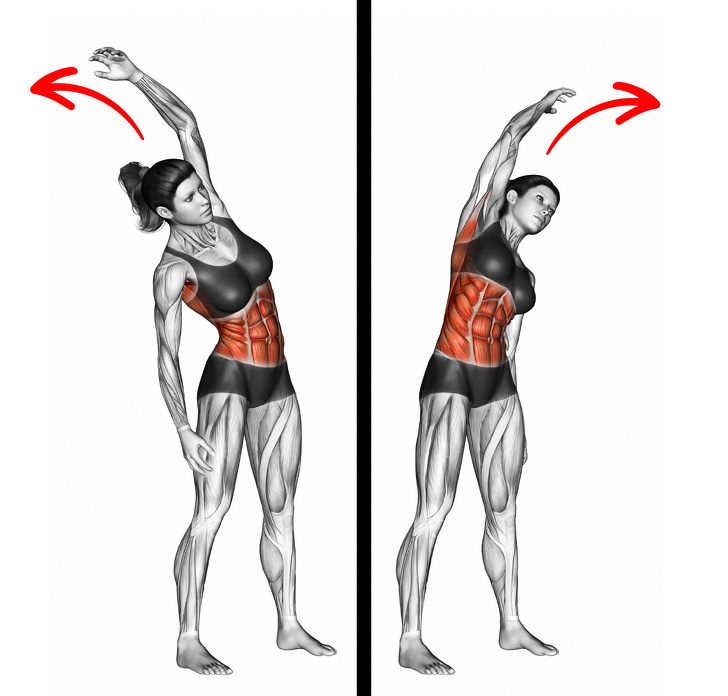
Наклоны вперед из положения стоя — развиваем гибкость

Главная » База упражнений

054. 7к.В закладки: Ctrl+D, Cmd+D

4.1

(167)

FitNavigator.ru/ редакция

Материал подготовлен командой сайта при поддержке наших экспертов: спортсменов, тренеров и специалистов по питанию.

Содержание статьи

Время на чтение: 3 мин.
1. Зачем делать?
2. Противопоказания
3. Техника выполнения

Наклоны вперед это простое, известное многим еще с детства упражнение, которое позволяет развить гибкость позвоночника и привести в тонус мышцы пресса, спины и ягодиц. Кроме того, это упражнение включено в нормы ГТО. Поэтому для всех тех, кто хочет иметь красивое гибкое тело и гордиться своей физической формой, выполнение наклонов вперед — обязательный пункт программы.

Зачем делать?

Наклон туловища вперед — вполне естественное движение для человеческого тела. Выполнение упражнения не требует ни какой-либо физической подготовки, ни спортивного инвентаря. Оно идеально для самостоятельных тренировок, в домашнем формате.

Влияние на организм:

• Наклоны туловища вперед улучшают гибкость позвоночника и подвижность тазобедренных суставов.
• Происходит тренировка растяжки подколенных сухожилий и мышц задней поверхности бедер. В особенности если вы делаете упражнение с прямыми ногами.
• Укрепление мускулатуры пресса, спины, ягодиц.
• Улучшение кровообращения, профилактика заболеваний сосудов головы.

Противопоказания

Справедливости ради стоит отметить, что наклоны вперед из положения стоя, как и любое другое упражнение имеют противопоказания. По сути, они связаны с двумя особенностями движения: перевернутым положением корпуса и воздействием на позвоночник. При некоторых состояниях организма эти воздействия нежелательны:

• Повышенное давление, головные боли, заболевания сосудов головы.
• Проблемы с позвоночником, при которых не рекомендуется напряжение мышц поясничной области.

Часто при проблемах с позвоночником рекомендуют не выходить в наклон из положения стоя, а поднимать таз из положения сидя на корточках, оставляя при этом руки внизу. За счет этого из упражнения исключается положение, когда корпус параллелен полу. Именно эта поза требует максимального напряжения мышц поясницы. Ведь когда вы уже наклонились, мышцы спины расслаблены.

Техника выполнения

Несмотря на популярность упражнения, техника его выполнения имеет свои особенности. Рассмотрим ее подробнее.

• Встаньте ровно, поставьте стопы на ширине плеч, выпрямите спину. В пояснице должен сохраняться естественный прогиб, грудная клетка должна быть расправлена.
• Напрягите пресс и, поддерживая спину прямой, опустите корпус вниз, провернувшись в тазобедренных суставах. Если ваш нынешний уровень гибкости не позволяет достать руками пола, спину не скругляйте, а немного согните ноги в коленях. Гибкость со временем разовьется, и вы сможете полноценно выполнить наклон вперед с прямыми ногами.
• Задержитесь в нижней точке на 1—2 секунды и за счет усилия ягодичных мышц вернитесь в исходное положение. Выполните нужное количество повторов.

Все время акцентируйте внимание на том, что вы не тянете корпус вверх за счет мышц спины. Это не только неправильно, но и травмоопасно. Мышцы спины держат корпус в прямом положении, а поднимают его ягодичные мышцы.

Также, выполняя наклоны туловища вперед, следует уделить внимание дыханию. На этот счет мнения специалистов расходятся. Самый простой и безопасный вариант – придерживаться анатомических особенностей человеческого тела. А именно – в положении стоя грудная клетка расправлена, легкие могут вместить в себя достаточный объем воздуха. В нижней точке, наоборот. Поэтому, логично опускать корпус на выдохе и поднимать его на вдохе.

https://www.youtube.com/watch?v=VxQsvDHAKtM

Начать можно с выполнения 10—15 наклонов в 2—3 подхода. Делать упражнение следует в медленном темпе, без рывков, полностью подконтрольно. Стремитесь к тому, чтобы из положения стоя опуститься в наклон с прямыми ногами.

Была ли статья для вас полезна?

Пожалуйста, оцените!

Очень жаль, что статья не была для вас полезна.

Просим вашего совета!

Расскажите, как мы можем улучшить материал?

Спасибо за ваш отзыв!

Гибкость Растяжка

FitNavigator.ru/ редакция

Материал подготовлен командой сайта при поддержке наших экспертов: спортсменов, тренеров и специалистов по питанию.

Поделиться:

Algebra 1 Help

Студенты, нуждающиеся в помощи по алгебре 1, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре 1.
Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по Алгебре 1.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации по алгебре 1.

• Алгебра 1

• Распределительная собственность

• Как использовать FOIL в дистрибутивной собственности

• Как использовать метод сетки для FOIL

• Уравнения / Неравенства

• Системы уравнений

• Уравнения/наборы решений

• Как разложить уравнение на множители

• Как найти решение set

• Как найти решение системы уравнений

• Линейные/рациональные уравнения/уравнения с переменными

• Как узнать, когда уравнение не имеет решения

• Как найти решение рационального уравнения с LCD

• Как найти решение уравнения

• Квадратные уравнения

• Как разложить на множители квадратное уравнение

• Как найти решение квадратного уравнения

• Системы неравенств

• Как найти решение неравенства со сложением

• Как найти решение неравенства с делением

• Как найти решение неравенства с умножением

• Как найти решение неравенства с вычитанием

• Функции и линии

• Алгебраические функции

• Как найти прямой вариант

• Как найти f(x)

• Как найти обратную вариацию

• Как найти домен функции

• Как использовать квадратичную функцию

• Уравнения прямых

• Формула средней точки

• Как найти концы отрезка

• Как найти середину отрезка

• Параллельные линии

• Как узнать, параллельны ли прямые

• Как найти уравнение параллельной прямой

• Как найти наклон параллельных прямых

• Перпендикулярные линии

• Как узнать, перпендикулярны ли прямые

• Как найти уравнение перпендикулярной прямой

• Как найти наклон перпендикулярных линий

• Точки и формула расстояния

• Как узнать, находится ли точка на прямой с уравнением

• Как найти длину линии по формуле расстояния

• Уравнения наклона и линии

• Как найти наклон линии

• Как найти уравнение прямой

• Графика

• Как построить график функции

• Как построить линию

• Как нарисовать точку

• Как построить график квадратичной функции

• Как построить график двухшагового неравенства

• Как построить график функции абсолютного значения

• Как построить график экспоненциальной функции

• Как построить график упорядоченной пары

• последовательности

• Как найти последовательные целые числа

• Как найти ответ на арифметическую прогрессию

• Как найти общую разницу в последовательностях

• Как найти следующий член арифметической прогрессии

• Как найти n-й член арифметической прогрессии

• Линейные уравнения

• Преобразование измерений

• Как решать уравнения абсолютного значения

• Как решить одношаговые уравнения

• Как решать двухшаговые уравнения

• Как писать выражения и уравнения

• Проценты

• Пропорции

• Линейные неравенства

• Неравенства абсолютного значения

• Графические неравенства

• Запись неравенств

• Проценты

• Десятичные числа и проценты

• Как найти десятичный эквивалент процента

• Как найти процент эквивалентный десятичной дроби

• Дроби и проценты

• Как найти дробь от процента

• Как найти дробные проценты

• Как найти процент от дроби

• Денежный процент

• Как найти размер прибыли

• Как найти простые проценты

• Как найти сумму налога с продаж

• Как узнать цену продажи

• Процент изменения

• Как найти процент уменьшения

• Как найти процент увеличения

• Целое и часть

• Как найти часть от целого в процентах

• Как найти целое из части с процентами

• Реальные числа

• Подсчет/наборы

• Как найти недостающее число в наборе

• Как найти количество целых чисел между двумя другими целыми числами

• Целочисленные операции

• Как складывать целые числа

• Как делить целые числа

• Как умножать целые числа

• Как вычитать целые числа

• Количество линий и абсолютное значение

• Как найти абсолютное значение

• Как найти значение с числовой строкой

• Как построить график неравенства с числовой прямой

• Как построить дроби на числовой прямой

• Статистика и вероятность

• Как найти межквартильный размах

• Как найти среднее

• Как найти медиану

• Как найти режим

• Как найти диапазон

• Как найти стандартное отклонение

• Переменные

• мономы

• Как делить одночленные частные

• Как умножить одночлен на многочлен

• Как умножать одночленные частные

• Многочлены

• Биномы

• Как найти решение рационального уравнения с биномиальным знаменателем

• Как найти решение биномиальной задачи

• Как найти значение коэффициента

• Как умножать биномы с распределительным свойством

• Как упростить биномы

• Факторные полиномы

• Как разложить многочлен на множители

• Как факторизовать переменную

• Полиномиальные операции

• Как складывать многочлены

• Как делить многочлены

• Как найти степень многочлена

• Как умножать многочлены

• Как вычитать многочлены

• Трехчлены

• Как складывать трехчлены

• Как делить трехчлены

• Как разложить трехчлен на множители

• Как умножать трехчлены

• Как вычитать трехчлены

Алгебра I часто впервые знакомит учащихся с процессами вычисления переменных, понимания неравенств и использования порядка операций для упрощения выражений. Некоторым учащимся часто бывает трудно освоить эти новые навыки; однако усердная практика основных алгебраических принципов жизненно важна для успеха в дальнейших курсах математики. Понимание геометрии, предварительного исчисления, исчисления и высшей математики, физики и химии требует фундаментального понимания того, как упростить выражения и манипулировать переменными. Нужны ли вам лучшие репетиторы по алгебре 1 в Бостоне, репетиторы по алгебре 1 в Детройте или лучшие репетиторы по алгебре 1 в Далласе, Форт-Уэрт, работа с профессионалом может вывести ваше обучение на новый уровень.

В общем, Алгебра I фокусируется на основах понимания и упрощения задач. Учащиеся работают над тем, чтобы логически продумать этапы решения проблемы, не делая немедленных выводов или решений. Кроме того, учащихся учат объяснять отношения между уравнениями, давать словесные описания графиков, таблиц и диаграмм и предсказывать форму фигур на основе математических соотношений. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре 1, которые помогут вам в самостоятельном обучении.

Общие темы по алгебре I включают:

• Арифметика с полиномиальными и рациональными выражениями: учащимся предлагается упростить числовые выражения с помощью порядка операций, разложить переменные в числовые уравнения и упростить сложные выражения с помощью различных комбинаций чисел и переменных.

• Создание выражений: используя графики и таблицы в качестве руководства, учащимся предлагается определить взаимосвязь между двумя или более переменными. Например, учащимся может быть предоставлена ​​таблица пройденного расстояния и времени, необходимого для преодоления этого расстояния. Ожидается, что учащиеся определят, как пройденное расстояние влияет на затраченное время (удвоение пройденного расстояния требует удвоения времени при той же скорости).

• Рассуждения с помощью уравнений и неравенств: учащиеся, изучающие алгебру I, должны найти значение переменных, упрощая числовые выражения. Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения.

• Видение структуры в выражении: использование рассуждений с помощью уравнений и неравенств в качестве основы, учащихся учат писать алгебраические выражения и неравенства на основе графиков, а иногда и таблиц данных.

Ключом к успеху в алгебре I является постоянная практика. В то время как некоторые учащиеся будут иметь опыт упрощения выражений, добавление графиков, диаграмм, неравенств и факторизации будет новым для других. Общие стратегии достижения успеха включают просмотр кратких резюме в учебниках перед выполнением домашних заданий и отработку дополнительных 10–15 заданий после выполнения назначенных отрывков домашнего задания. Часто учащиеся изучают шаблоны, необходимые для решения задач, путем постоянного повторения вместо того, чтобы читать разделы книги. Наличие другого метода материального подкрепления в дополнение к обучению в классе и домашнему заданию обычно полезно для большинства учащихся. В дополнение к справочному разделу по алгебре 1 и урокам по алгебре 1 вы также можете рассмотреть некоторые из наших карточек по алгебре 1.

Если вы хотите укрепить свои знания по алгебре I, решая практические задачи, ознакомьтесь с бесплатными ресурсами по алгебре I от Varsity Tutors. Каждая практическая задача сопровождается подробным пошаговым ответом, поэтому, если вы пропустите какой-либо из них, вы сможете точно определить, где в своих расчетах или рассуждениях вы ошиблись, и избежать повторения этой ошибки позже. Практические задачи также организованы по понятиям, поэтому, если у вас возникают трудности с графическим отображением линейных функций или порядком операций, вы можете отвечать на вопросы только по этим темам, не перебирая материал, который будет полезен для ваших конкретных учебных потребностей. Бесплатные практические задачи по алгебре I от Varsity Tutors помогут вам получить дополнительную практику, которая вам нужна при сдаче или повторении алгебры I!

Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона
(бесплатный онлайн-инструмент вычисляет уклон с учетом 2 баллов)

Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.

Разные слова, та же формула

Учителя используют разные слова для координат y и координат x.

1. Некоторые называют координаты у подъемом, а координатами х — бег.
2. Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .

Все эти слова означают одно и то же , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!

Пример 1

Наклон прямой , проходящей через точки (1, 2) и точки (4, 3), равен $$ \frac{1}{3}$$.

Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.

Может ли любая точка быть $$( x_1 , y_1 ) $$ ?

Есть только один способ узнать!

Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .

Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .

Работа рядом

точка (4, 3) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$

точек (1, 2) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$

Ответ: , а не не имеет значения, какую точку поставить первой. Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом!
$$ \фракция{1}{3} $$

Пример 2 наклона линии А

Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Видеоруководство по наклону линии

Наклон вертикальных и горизонтальных линий

Наклон вертикальной линии не определен

Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).

Наклон горизонтальной линии равен нулю

Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль. Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».

Любые две точки на прямой имеют одинаковый наклон?

Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.

Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать любых 2 точек на линии.

Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.

Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.

Наклон линии

Никогда не меняется

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона
(бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Практика Проблемы

Проблема 1

Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$

$
\frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3}
\\
= \ в коробке {-2 }
$

Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$

$ \frac{3- \red 9{10- \красное 7}
\\ =\ гидроразрыв{-6}{3}
\\
= \в коробке{-2}
$

Проблема 2

Прямая проходит через (4, -2) и (4, 3). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$

$
= \frac{-2 — \red 3}{4- \red 4}
«=»
\frac{-5}{\color{red}{0}}
\\ = \text{неопределенный}
$

Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$

$
= \frac{3- \red{-2}}{4- \red 4}
«=»
\frac{5}{\color{red}{0}} \\
= \текст{неопределенный}
$

Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.

Проблема 3

Прямая проходит через (2, 10) и (8, 7). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$

$
\frac{10 — \red 7}{2 — \red 8}
\\ = \ гидроразрыва {3}{-6}
\\ = -\фракция{1}{2}
$

Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$

$
\frac{7 — \red {10}}{8- \red 2}
\\ = \ гидроразрыв {-3} {6}
\\ = -\фракция{1}{2}
$

Проблема 4

Прямая проходит через (7, 3) и (8, 5). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$

$$
\frac{ 5- \red 3}{8- \red 7}
\\
= \ гидроразрыва {2} {1}
\\ = 2
$$

Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$

$$
\frac{ 3- \red 5}{7- \red 8}
\\= \фракция{-2}{-1}
\\ = 2
$$

Проблема 5

Прямая проходит через (12, 11) и (9, 5) . Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$

$$
\frac{ 11 — \red 5}{12- \red 9}
\\ = \ гидроразрыва {6} {3}
\\ =2
$$

Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red{ 11} }{9- \red { 12}}
\\ = \фракция{-6}{-3}
\\ = 2$$

Проблема 6

Каков наклон линии, проходящей через (4, 2) и (4, 5)?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$

$$
\frac{ 2 — \red 5}{4- \red 4}
\\ = \frac{-3}{\color{red}{0}}
\\ = не определено
$$

Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$

$$
\frac{ 5 — \red 2}{4- \red 4}
\\ = \frac{ 3}{\color{red}{0}}
\\ = не определено
$$

ПРЕДУПРЕЖДЕНИЕ! Сможете ли вы уловить ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ . У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?

Задача-вызов

Найдите наклон прямой через две точки.

Попытка №1

$
наклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
«=»
\ гидроразрыв {6-3} {1-2}
\\= \фракция{3}{-1}
=\в коробке{-3}
$

Попытка #2

$$
наклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
«=»
\фракция{6-3}{2-1}
\\= \фракция{3}{1}
\\
= \в коробке{3}
$$

Попытка №3

$$
уклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
\\ =\ гидроразрыва {2-1} {6-3}
\\ =\в коробке{ \frac{1}{3}}
$$

Правильный ответ — попытка №2.

В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:

$$
\frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}}
$$

Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!

$$
\ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}}
$$

Тренировка склонов Генератор проблем

Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.